Graph or Statistics That Says Numbers Numbers Funny
What does/doesn't follow Benford's law
An analysis of hundreds of sets of numbers from Wikidata.

Like many others, the first time I heard about Benford's law, I thought: "What? That's weird! What's the trick?" And then, there is no trick. It is just there. It is a law that applies for no apparent good reason.
If you have never heard of it, let's look at what it is: Imagine a set of numbers from some real-life phenomenon. Say, for example, the populations of all inhabited places on Earth. There would be thousands of numbers, some very big, some very small. Those numbers exist not because of some systematic process but somehow emerged out of the thousands of years of the lives of billions of people. You would therefore expect them to be almost completely random. Thinking about those numbers, if I asked you: "How many of them start with the digit 1, compared to 2, 3, 4, etc.", intuitively you would probably say: "more or less just as many". You would be wrong. The answer is: significantly more.
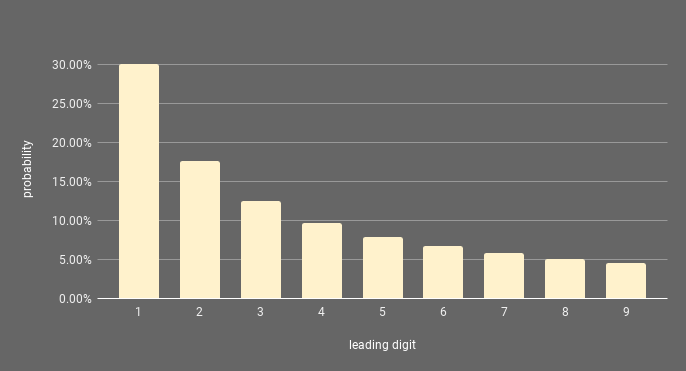
According to Benford's law (which should really be called Newcomb–Benford law, see below), in large sets of naturally-occurring numbers spanning across multiple orders of magnitude, the leading digit of any number is much more likely to be small than big. How more likely? Formally, the probability P(d) that a number starts with the digit d is given by:
P(d) = log10(1+1/d)
That means that in those sets of naturally-occurring numbers, the probability that a number will start with 1 is just over 30%, while the probability that it will start with 9 is just under 5%. Weird right?
This strange natural/mathematical phenomenon was first discovered by Simon Newcomb (hence the complete name) who noticed that the pages at the beginning of books containing logarithmic tables, which start with 1, were much more worn out than the pages at the end (starting with 9). Based on this observation, showing that people tended to need logarithmic tables more often for numbers starting with 1, he first formulated what is now known as the Newcomb-Benford law, although with a slightly different formula for the probability of the first digit. It was re-discovered by Frank Benford more than 65 years later, and tested on several different things, including populations in the US. Since then, it has been tested on and applied to many things, from financial fraud detection to code, parking spaces or even COVID. The idea is that if a set of numbers occur or emerge naturally, without being doctored or somehow artificially constrained, there is a good chance they will follow Benford's law. If they don't follow the law, there is something fishy.
But is this really universally true, and to what extent? We can assume that numbers representing different phenomena follow Benford's law to a different extent, sometimes more, sometimes less, and sometimes not. So the question is:
What follows Benford's law, and perhaps more importantly, what does not?
To answer that, we need a lot of those sets of naturally-occurring numbers.
Wikidata to the rescue
Newcomb and Benford were not quite as lucky as we are. To find sets of numbers on which to test their law, they had to manually collect them from whatever source was available. Nowadays, not only do we have a universally accessible encyclopedia of everything, we have a data version of it: Wikidata.
Wikidata is the Wikipedia of data. It is a crowdsourced database of, if not everything, quite a big part of it. It is possible for example using Wikidata to quickly obtain, with a relatively simple query, the size of the populations of every US cities and many, many more things. It should therefore also be possible to obtain all the sets of numbers it contains.
To do that, we use the RDF-based representation of Wikidata. RDF (Resource Description Framework) is a graph-based data representation for the web. Basically, things in RDF are represented by URIs, and connected by labelled edges to other things or values. For example, the figure below shows a simplified extract of what the representation of the city of Galway, located in Ireland and with a population of 79,504 people looks like in Wikidata's RDF.
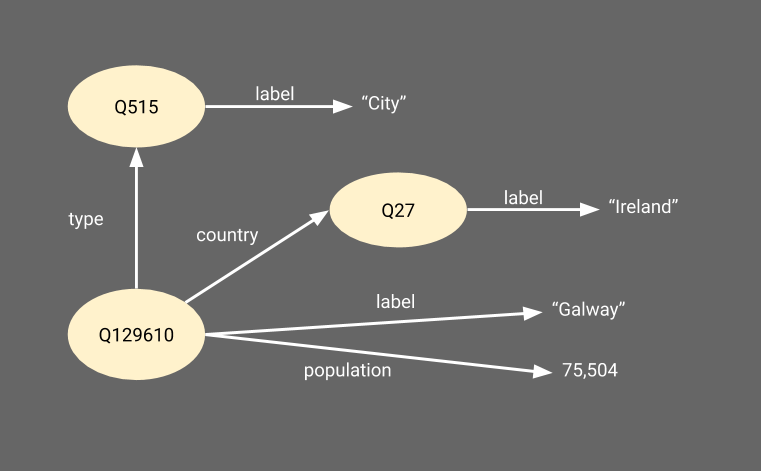
The nice thing about RDF is that a very, very large graph, can be represented by a set of triples of the form <subject,predicate,object>. Each of those triples corresponds to an edge in the graph, and represents one atomic piece of information.
<http://www.wikidata.org/entity/Q129610> <http://www.w3.org/2000/01/rdf-schema#label> "Galway" . <http://www.wikidata.org/entity/Q129610> <http://www.w3.org/1999/02/22-rdf-syntax-ns#type> <http://www.wikidata.org/entity/Q515> . <http://www.wikidata.org/entity/Q515> <http://www.w3.org/2000/01/rdf-schema#label> "City" . <http://www.wikidata.org/entity/Q129610> <http://www.wikidata.org/entity/P17> <http://www.wikidata.org/entity/Q27> . <http://www.wikidata.org/entity/Q27> <http://www.w3.org/2000/01/rdf-schema#label> "Ireland" . <http://www.wikidata.org/entity/Q129610> <http://www.wikidata.org/entity/P1082> "75,504"^^<http://www.w3.org/2001/XMLSchema#Integer> .
So the first step in collecting sets of numbers from Wikidata is to extract all the triples for which the object part is a number.
We start by downloading the full dump of the entire Wikidata database as a compressed NTriples (NT) file. NT is a terribly inefficient representation of RDF where each triple is represented in a line. The GZipped file to download (latest-all.nt.gz) is quite large (143GB) and I would not recommend trying to uncompress it. However, because each triple is represented completely independently from the rest on one line, this format makes it very easy to filter the data with basic linux command-line tools without having to load the whole thing in memory. So, to extract triples which objects are numbers, we use zgrep (grep that works on GZipped files) to find triples that have a reference to the decimal, integer or double types in the following way:
zgrep "XMLSchema#decimal" latest-all.nt.gz > numbers.decimal.nt
zgrep "XMLSchema#double" latest-all.nt.gz > numbers.double.nt
zgrep "XMLSchema#integer" latest-all.nt.gz > numbers.integer.nt Then we can put all of those together using the cat command:
cat numbers.decimal.nt numbers.double.nt numbers.integer.nt > numbers.nt And check how many triples this 110GB file ends-up containing by counting the number of lines in it:
wc -l numbers.nt
730238932 numbers.nt Each line is a triple. Each triple as a number as value (object). That's a lot of numbers.
The next step is to organise those numbers into meaningful sets and count how many in each set start with 1, with 2, with 3, etc. Here, we use the "predicate" part of the triple. There are, for example, 621,574 triples in this file that have < http://www.wikidata.org/entity/P1082 > as predicate. http://www.wikidata.org/entity/P1082 is the property Wikidata uses to represent the population of inhabited places. So we can group all of those, and make it into the set of all populations known to Wikidata. That will be one of the naturally occurring sets of numbers that we will test.
The simple python script below creates a JSON file with the list of properties, the number of triples of which they are predicate, the minimum and maximum numbers those triples have as values, the number of orders of magnitude they cover, and the number of numbers starting with 1, 2, 3, etc.
import time
import json
import re data = {} st = time.time()
with open("numbers.nt") as f:
line = f.readline()
count = 0
while line:
p = line.split()[1]
val = int(re.findall("\d+", line.split()[2])[0])
val1 = str(val)[0]
if p not in data:
data[p] = {"i": val, "a": val, "c": 0, "ns": {}}
if val < data[p]["i"]: data[p]["i"] = val
if val > data[p]["a"]: data[p]["a"] = val
if val1 not in data[p]["ns"]: data[p]["ns"][val1] = 0
data[p]["ns"][val1] += 1
data[p]["c"] += 1
count += 1
line = f.readline()
if count % 1000000 == 0:
print(str(count/1000000)+" "+str(len(data.keys()))+" "+str(time.time()-st))
st = time.time()
if count % 10000000 == 0:
with open("numbers.json", "w") as f2:
json.dump(data, f2)
with open("numbers.json", "w") as f2:
json.dump(data, f2)
We obtain 1,582 properties in total, representing as many sets of numbers to be tested against Benford's law. We reduce this to 505 properties as there are several redundant representations of the same relation into properties in Wikidata. We also extract in another script the label (name) and description of each of the properties, so we don't have to look them up later.
Testing for Benfordness
Now that we have many sets of numbers, and their distributions according to their leading numbers, we can check how much they follow Benford's law. Several statistical tests can be used to do this. Here, we use a relatively simple one called Chi-Squared. The value of this test for a set of numbers is given by the formula
χ² = Σᵢ(oᵢ-eᵢ)² / eᵢ
Where i is the leading number under consideration (1 to 9), oᵢ is the observed value for i (the percentage of numbers in the set that start with i) and eᵢ is the expected value (the percentage of numbers that should start with i according to Benford's law). The smaller the result is, the more Benford the set of numbers is. The script below calculates the Chi-Squared test on each set of numbers created with the previous script, to check how they fit Benford's law.
import math
import sys
import json if len(sys.argv) !=2:
print("provide filename")
sys.exit(-1) es = {
"1": math.log10(1.+1.),
"2": math.log10(1.+(1./2.)),
"3": math.log10(1.+(1./3.)),
"4": math.log10(1.+(1./4.)),
"5": math.log10(1.+(1./5.)),
"6": math.log10(1.+(1./6.)),
"7": math.log10(1.+(1./7.)),
"8": math.log10(1.+(1./8.)),
"9": math.log10(1.+(1./9.))
} print("expected values: "+str(es)) data = {}
with open(sys.argv[1]) as f:
data=json.load(f) for p in data:
sum = 0
for n in es:
if n in data[p]["ns"]:
sum += data[p]["ns"][n]
cs = 0.
for n in es:
e = es[n]
a = 0.
if n in data[p]["ns"]:
a = float(data[p]["ns"][n])/float(sum)
cs += (((a-e)**2)/e) # chi-square test
data[p]["f"] = cs with open(sys.argv[1]+".fit.json", "w") as f:
json.dump(data, f)
So, is it real?
The results obtained are available in a Google Spreadsheet for convenience. The scripts and results are also available on Github.
The first thing to notice when looking at the results is that our favourite example, population, does very very well. It is in fact the second best fit for Benford's law with a Chi-Squared value of 0.000445. There are over 600K numbers in this, which just happen to exist, and they follow almost exactly what Benford's law predicted. With such a low value for the Chi-Squared test and such a large sample, the chances that this could be a coincidence are so small, they are truly impossible to contemplate. It is real.
Unsurprisingly, several other properties very related to population also all end up in the top-10 most fitting Benford's law, including literate/illiterate populations, male/female populations or number of households.
The question I'm sure everybody is dying to see answered is "which property is first then?", since population is only second. With a Chi-Squared of 0.000344, the first place actually goes to a property called number of visitors which is described as the "number of people visiting a location or an event each year" (48,908 numbers in total).
Amongst the very highly Benford, we also find area (the area occupied by an object), or total valid votes (for elections. The number of blank votes is also doing well on Benfordness).
There seem also to be quite a few properties related to diseases in the highly Benford properties in Wikidata, including number of cases, number of recoveries, number of clinical tests, and number of deaths.
Numbers related to companies also appear very strongly amongst the top Benford properties. The property employees (the number of employees of a company) is the strongest among those, but we also see patronage, net income, operating income, and total revenue.
Sports statistics make a good appearance, with total shots in career, career plus-minus rating and total points in career, together with several biology- and other nature-related topics, such as wingspan (of aeroplanes or animals), proper motion (of stars), topographic prominence (i.e. the height of a mountain or hill) or distance from Earth (of astronomical objects).
There are of course many more properties that fit Benford's law very well: The ones above only cover the very top most fitting sets of numbers (with a Chi-Squared below 0.01). They are also not particularly surprising as they match very well the characteristics of sets of numbers that should normally follow Benford's law: They are large (the smallest, number of blank votes, still contains 886 numbers), cover several orders of magnitudes (from 3 to 80) and, more importantly, are naturally occurring: They are not generated through any systematic process. They just emerged.
There is one very significant exception to this however. With a Chi-Squared value of 0.00407, and 3,259 numbers covering 7 orders of magnitude, we find the property Alexa rank. This corresponds to the ranking of websites from the Alexa internet service, which provides information about websites based on traffic and audiences. It is very hard to explain how it could fit so well, since, being a ranking, it should normally be linearly distributed from 1 to its maximum value. There are two possible explanations however as to why this happened: 1- For a given website, several rankings might be available for several years, and 2- not all websites ranked by Alexa are in Wikidata. In other words, it is not the ranking itself that follows Benford's law, but the naturally occurring selection of rankings in Wikidata. The same kind of things, worryingly, might affect other results too and is a good example demonstrating how any dataset might be biased in a way that seriously affects the results of statistical analyses.
How about the bad ones?
So, we have verified that Benford's law indeed applies to many naturally occurring sets of numbers, and even sometimes to naturally occurring selections of non-naturally occurring numbers. What about the cases when it does not work?
First, we can eliminate all the sets that are too small (less than 100 numbers) and that cover too few orders of magnitude (less than 3). Those, in most cases, would not fit at all, and if they do, we cannot rule out the possibility that it is just a coincidence.
The worst-fitting property of the whole set we looked at is lowest atmospheric pressure, described as the "minimum pressure measured or estimated for a storm (a measure of strength for tropical cyclones)", with a Chi-Squared of 12.6. The set contains 1,783 numbers varying from 4 to 1,016. While this is a naturally occurring set of numbers that match the needed characteristics, it is easy to see why it does not fit. Atmospheric pressure does not usually vary that much, and it can be expected that most of the values are actually close to the average sea-level pressure (1013 mbar). It is even possible that the value of 4 is simply an error in the data.
Many other of the non-fitting properties can be explained similarly: Their values usually don't vary enough for them to follow Benford's law, but exceptions and outliers make that they still span several orders of magnitude. Those include wheelbase (distance between front wheels and rear wheels on a vehicle), life expectancy (of species), field of view (of a device for example), or mains voltage (in a country or region).
Interestingly (maybe because I know nothing about astronomy), while related to natural phenomena, many of the badly fitting properties correspond to measures related to planets or space: semi-major axis of an orbit, effective temperature (of star or planet), apoapsis (distance at which a celestial body is the farthest to the object it orbits), periapsis (distance at which a celestial body is the closest to the object it orbits), metallicity (abundance of elements that are heavier than hydrogen or helium in an astronomical object) and orbital period (the time taken for a given astronomic object to make one complete orbit about another object). Maybe Benford's law is a law of Earth's nature, or even of human nature, rather than a law of the universe.
If that's the case however, there is an interesting exception here: Within the really badly fitting properties, we find number of viewers/listeners (number of viewers of a television or broadcasting program; web traffic on websites). This set includes 248 numbers, ranging from 5,318 to 6 billion. This feels very paradoxical considering that the Alexa rank (which is related to the size of the audience for websites) was also our exception for well-fitting properties. Maybe the same explanation applies however: If we had a complete set of numbers of subscribers/viewers for everything, it might follow Benford's law very well, but we don't and the bias introduced by the selection of those 248 ones, which might focus on the most noticeable websites and programs, is a sufficiently unnatural constraint that it makes it lose its Benfordness.
So?
Benford's law is weird. It is unexpected and not well explained, but somehow actually works. There is clearly a category of sets of numbers that are supposed to follow Benford's law, and in effect very much do so. There are also others that apparently don't and in most cases, it is relatively easy to know why. Interestingly however, there are a few cases where numbers don't behave the way they should with respect to Benford's law. As mentioned at the beginning of this article, this phenomenon as been extensively used to detect when numbers have been doctored, by checking for numbers that should follow Benford's law and in effect do not. It seems that there is another category of applications looking at selections of numbers that should not follow Benford's law. If they do, it might be an indication that what may very well look like random sampling somehow emerges to be biased by the natural tendencies that uncontrolled human and natural processes have to produce highly Benford numbers. Knowing this, and in which category a dataset is supposed to fall could be very useful to test data against such biases and the representativeness of data samples.
And of course, there is the case of astronomy. I suspect the answer would simply emphasize my own ignorance in the matter, but I would really like to know why all those measures related to astronomical bodies so stubbornly refuse to obey Benford's law.
Source: https://towardsdatascience.com/what-does-doesnt-follow-benford-s-law-7d0b3c14afa5
0 Response to "Graph or Statistics That Says Numbers Numbers Funny"
Post a Comment